Is the Universe a Computer? - Part I
Unravelling the true nature of the Cosmos, one bit at a time.

Let’s kick off 2026 with a thought experiment.
You’ve all heard the Simulation Hypothesis by now, right? The idea that we might just characters in a high-res version of The Sims running on a supercomputer in some teenager’s basement in another dimension.
Well, this is not that.
The simulation hypothesis is a fun thought experiment, and it’s certainly great for selling movie tips, but I think it misses the point entirely. It presumes an outside that we can never reach. But we don’t need to posit any external observer, a higher-dimensional teenager in a basement. What if the universe isn’t inside a computer; but it is itself a computer.
This is a serious metaphysical position held by several prominent thinkers known as pancomputationalism, which basically means everything there is, is just computation. In this and a follow up article, I want to run with this argument and stretch it to its ultimate implications. Not necessarily because I believe it (I will tell you exactly what I believe at the end) or because I want you to believe it.
No, I just honestly think this is a very intellectually engaging argument to discuss, and even if it ends up not being true in its ultimate form (which we shall see), it presents some pretty damn cool ideas–and some pretty horrific ones. So even if just as a fun thought experiment, I invite you to ponder on it for a while.
You may be surprised by what you discover.
The Universe as a Universal Computer
To understand pancomputationalism, we have to go back to the 1980s, to a physicist-turned-polymath named Stephen Wolfram staring at a computer screen.
Wolfram was playing with something called Cellular Automata—incredibly simple programs that live on a grid of pixels. You start with a line of black and white squares and give them a rule: “If your neighbor is black and you are white, turn black in the next step.” It sounds like a toy or perhaps something you’d learn in a mid-school basic coding class.
CAs where not Wolfram’s invention. We can trace them back to Stanislaw Ulam and the polygenious John von Neumann back in the 1940s (because of course anything you find interesting in late 20th century was actually invented by von Neumann!) but it wasn’t until the 70s when John Conway brought them to the public’s attention with a series of puzzles about a specific form of 2-dimensional CA called Game of Life.
The following picture shows a “Glider Gun”, one of the most interesting patterns that answers one of Conway’s original questions: the existence of configurations that ran forever without looping (you can see how the small thingies that are thrown diagonally—called gliders—keep moving forever).
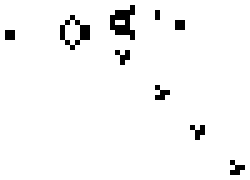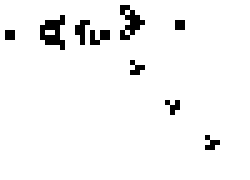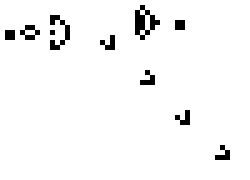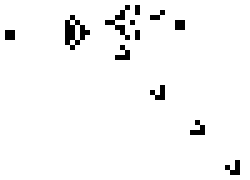
The reason these are interesting, among other things is because depending on the initial configuration, there are several, qualitatively distinct developments a cellular automaton can follow. Wolfram classified them into 4 more-or-less well-defined classes.
Classes 1 and 2 corresponding to different ways in which the initial configuration converges to a stable configuration (like the Glider Gun) that may or not keep evolving, but in a very controlled, predictable way. Some of these eventually stop, others keep going forever, but always in a very structured form.
Class 3, in contrast, is chaotic, random, unpredictable. In fact, several configurations in this category are thought to be cryptographically-secure random generators—the strongest kind of randomness you can get from a deterministic set of rules.
And then there is Class 4, a category of CA configurations that exhibit such a degree of complexity in their evolution that Wolfram conjectured most if not all configurations in this category where capable of general-purpose computation! Eventually, it was shown that extremely simple CAs do possess this trait, including one of Wolfram’s original CAs, Rule 110, and several configurations in Conway’s Game of Life.
The reason this is interesting for our discussion, is because it led some thinkers to ponder whether this kind of complexity born out of simplicity could be the explanation behind all of physics. The first one is perhaps Konrad Zuse, a German engineer who built the first programmable computer (the Z3) during World War II.
In his 1969 book Rechnender Raum (Calculating Space), he proposed that the universe is a discrete lattice. He argued that the infinities that plague quantum physics could be solved if we just admitted that space has a minimum pixel size. In Zuse’s vision, space isn’t an empty stage where things move around. Space is the computer itself. An electron isn’t a particle moving through the vacuum; it’s a propagating pattern on the spatial grid. Think of it like a glider in Conway’s Game of Life: the pixel doesn’t move, the information does.
This is the heart of Pancomputationalism. The idea that, deep down, the Universe is not a metaphorical clockwork machine but an actual digital computer, though not one made of transistors, of course. Wolfram takes this to an extreme, by positing all of physics can be derived from a simple computational model, a hypergraph of nodes and edges that change according to some specific rules. In this theory—which is perhaps the most advanced form of pancomputationalism—the underlying computational lattice is so intricate that extremely simple processes like one electron jumping from an energy state to another would require several trillions of operations.
But the details matter less than the general idea: if there are some extremely simple mechanism (like the Rule 110 CA) that can support general computation, then universal computers most be abundant in the Universe. As an example, the DNA molecule must be capable of universal computation!
So why not take this argument to its logical end? Perhaps this is all there is! Perhaps universal computation is the ultimate level of complexity. If that’s the case, then the whole Universe is ultimately just a very complex computer.
Time for some counter-arguments
Of course, the idea that the universe is just a computer—or more specifically, a Turing machine—is a hard pill to swallow for many. If the cosmos is indeed a digital lattice, then everything within it should be effectively computable. But nature has a way of throwing us curve balls that look suspiciously like hacks of the system. Processes that seem to require more than universal computation to work out.
Let’s check two of the most famous counter-arguments to pancomputationalism.
Black Holes and Hypercomputers
One of the most persistent challenges to pancomputationalism is the idea of Hypercomputation. The argument goes like this: one of the simplest ways to show something is more complex than a Turing machine is to show it can solve problems known to be computationally undecidable. The most famous of these is the Halting problem–the question of whether a given arbitrary computation will end up eventually.
This was proven by Alan Turing himself to be generally undecidable. That is, you cannot predict whether a computer program will eventually halt or run forever just by looking at its source code. You can do it for some programs (because the code has no loops, for example, or for some contrived mathematical property), but you cannot devise a single, universal rule—a computer program—that tells you without doubt whether another arbitrary program stops.
But you can simulate it! If you want to know whether a program ends, just run it. If it ends, then eventually you will know it. The problem is, if it doesn’t end, you will never know! You will just wait indefinitely, because you can never say “Ok, I’ve seen enough”, the program might just end next iteration.
Ok, so here’s the twist. This presumes each iteration takes a finite amount of time, so an infinite number of iterations must take an infinite time, so you cannot outwait it. But what if we could make each iteration take less and less time? Like, the first iteration takes 0.5 seconds, the next one 0.25 seconds, and so on, each iteration taking half of the previous one? If we had this magical computer that accelerates as it computes, we could finish an infinite amount of iterations in a finite time!
This is called hypercomputation, and is an extension of something called a hypertask to the realm of computational complexity. Hypertasks are like taking limits in real life. You perform each step slightly faster, in such a way that the infinite sum of smaller and smaller times converges to something finite. Much like Zeno’s paradox, but each step is not smaller, it’s just faster.
Can we have hypercomputers in the real world? Well, some physicists suggest that the extreme gravity of a special, theoretic kind of black holes could allow for supertasks. Imagine an observer orbiting a black hole while a computer falls into it. Because of the way gravity warps time, the falling computer, in its own timeframe, would spend eternity counting towards infinity. But we would observe all its infinite lifetime compressed into a finite amount of time.
This would be crazy! Imagine we want to know whether, e.g., Riehmann hypothesis—the most important unsolved problem in pure mathematics—is true. We would just make a program that would check all infinite zeros of the Zeta function, run it in a computer, and throw it into a black hole. As the computation stretches to infinity, we would know definitely whether any zero has real part different to 1/2, because the program would check them all in finite time!
We could solve almost any open mathematical problem this way!
Now, this does require some stretch of imagination, some bizarre physics that many don’t agree actually exists. These are not regular black holes, but a special kind of black hole that has never been observed. And of course we have to issue of actually building a computer than can last forever! But nevertheless, just proving the physical possibility of hypercomputation–even if impossible in engineering terms–would undermine the whole idea of pancomputationalism.
The Mind vs. The Machine
Then there is the challenge from the human side of the fence. Roger Penrose, in his seminal The Emperor’s New Mind, famously argued that human consciousness is fundamentally non-algorithmic.
His argument leans heavily on Gödel’s Incompleteness iheorem. Penrose claims that because we can “see” that a Gödelian statement is true—even though it’s unprovable within its own formal system—our brains must be doing something that transcends simple computation. He actually suggests that this “something” is a quantum gravity effect happening in the tiny structures of our brain called microtubules.
Critics like Scott Aaronson are quick to point out that even if our brains use quantum effects, that doesn’t necessarily make them hypercomputational. (A quantum computer, after all, is still just a computer, it just has a different complexity class). But Penrose’s argument hits on a deep-seated intuition: that phenomena such as love, consciousness, or creativity aren’t just very long strings of 1s and 0s. If this is true, then not only is the Universe itself uncomputable, but actually the most interesting human traits, perhaps even the root of intelligence itself, would be forever outside the reach of regular computers—no superintelligent AI for you, Sam Altman.
The Universe Hardware Spec
But for now, let’s run with the original argument. If we do assume the Universe is doing something akin to general computation, we can ask the next logical question? How long has this been going on? Not in years, of course–we kinda know that already–but in computational steps. How big is the Universal Hardware?
The question might seem bogus at first, but underneath this seemingly crazy assumption we will find some profound truths about the nature of computation. To even start to answer this we must link two seemingly separate realms: the digital and the physical.
We often think of information as something ethereal—software is just math, right? But in the 1960s, Rolf Landauer showed all us wrong. He realized that information is fundamentally tied to thermodynamics. Specifically, Landauer’s Principle states that any logically irreversible operation—like erasing a bit of information—must produce a specific amount of heat.
This isn’t the regular heat you feel when your computer works for too long, of course. That is just a byproduct of imperfect engineering–moving pieces with friction, electrical wiring with imperfect insulation, etc. No, this is much more fundamental. Even if you remove all sources of energy loss, the fact that two bits of information become one (when you and two boolean variables for example) means that some amount of energy is released, increasing the entropy of the system.
Thinking has a literal energy cost.
This gives us a maximum performance for any given physical computer: Bremermann’s Limit. Just take the total energy you input into the system, assume there are no extra losses, and you will still deplete that energy just doing computation. So, if the Universe is a computer, it must have this physical limit. After all, there is just so much energy in the Universe. How fast is the cosmic CPU?
If you take 1 kg of matter and turn it into the Ultimate Laptop, it can perform at most 1.36 × 1050 bits per second. That’s a staggering number—far beyond anything we can currently build—but it’s not infinite. It is a hard, physical ceiling. There is no “overclocking” the universe beyond the speed of light and the Planck constant.
When you scale this logic up to the entire observable universe, you get a spec sheet for reality that is both terrifying and humbling.
Physicist Seth Lloyd calculated that since the Big Bang, the entire universe has performed at most 10120 operations on roughly 1090 bits. To put that in perspective, there are some 1080 elementary particles in the observable universe, so each particle must be represented by something like 1010 bits. Huge, yes, but finite.
Where does this leave us?
If the Universe is indeed a computer, that has been running for a finite amount of time, and has thus performed a finite amount of computation, what can we say about the laws of physics. Are there things forever beyond the realm of Science.
This is question I want to answer next, but that will take us on a tour around some of the most important theoretical concepts in computer science. In the end, we will see that a Digital Universe has some damn horrifying constraints, but it also possesses some beautiful freedoms we can only dream of in an otherwise uncomputable Universe.
But that is a story for another Friday!



I quite agree pancomputationalism is a fun topic! On some level, it seems trivially true that the universe is "computing" itself. I think a key question is whether it is discrete or continuous, a digital computer or an analog computer. Theories like loop quantum gravity feature a discrete background, but GR and most QM suggest a continuous background.
A thing about those Life Gliders is that, as with all our algorithms, they are abstractions designed by an intelligence. My sense is that algorithms are the end of a long evolution process that first creates intelligences capable of abstractions like algorithms (and maths in general).
FWIW, I like Penrose's argument in TENM that mind doesn't seem algorithmic because Gödel. He suggests quantum effects in the book (Hameroff approached him because of it with his microtubules idea), but it could just be that brains are analog computers, not discrete ones. We can, in a sense, "take the mental limit" of an idea like Gödel's to a "divide by zero" true conclusion outside of computation.
Zuse came up with the idea earlier—around 1946-47, when he was in a village in Bavaria and his z4 computer was disassembled in a barn. As for the reception to the idea, he paraphrased Pauli’s comment on the reaction to quantum theory: “not that my idea was crazy; it was not crazy enough.”